Exponential
Attenuation
Home > Radiation
Protection and Quality Assurance > Radiation
Physics and Biology > Basic Properties of Radiation
Can we please get your advice on this one question?
The concept of exponential attenuation is relevant primarily to uncharged ionizing radiation (i.e., photons and neutrons), which lose their energy in relatively few large interactions, rather than charged particles which typically undergo many small collisions, losing their kinetic energy gradually. An individual uncharged particle has a significant probability of passing straight through a thick layer of matter without losing any energy, while a charged particle must always lose some or all of its energy.
An uncharged particle has no limiting “range” through matter, beyond which it cannot go; charged particles all encounter such a range limit as they run out of kinetic energy. For comparable energies, uncharged particles penetrate much farther through matter, on the average, than charged particles, although this difference gradually decreases at energies above 1 MeV. Consider a monoenergetic parallel beam consisting of a very large number N0 of uncharged particles incident perpendicularly on a flat plate of material of thickness L
Simple Exponential Attenuation:
• Assume for this ideal case that each particle either is completely absorbed in a single interaction, producing no secondary radiation, or passes straight through the entire plate unchanged in energy or direction
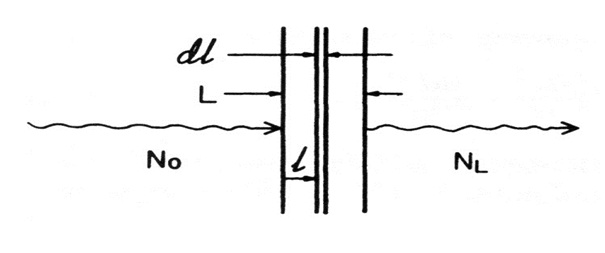
• Let (m×1) be the probability that an individual particle interacts in a unit thickness of material traversed
• The probability that it will interact in an infinitesimal thickness dl is mdl
• If N particles are incident upon dl, the change dN in the number N due to absorption is given by
dN = -µdl
where m is typically given in units of cm-1 or m-1, and dl is correspondingly in cm or m
• The fractional change in N due to absorption of particles in dl is just
dN/N = -µdl
• Integrating over the depth l from 0 to L, and corresponding particle populations from N0 to NL, give
• This is the law of exponential attenuation, which applies either for the ideal case described above (simple absorption, no scattering or secondary radiation), or where scattered and secondary particles may be produced but are not counted in NL
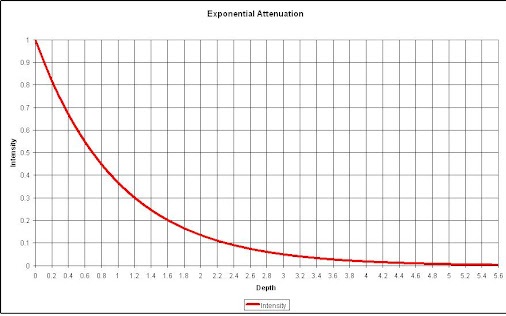
• The quantity m is called the linear attenuation coefficient, or simply the attenuation coefficient
• When it is divided by the density r of the attenuating medium, the mass attenuation coefficient m/r (cm2/g or m2/kg) is obtained
• m is sometimes referred to as the “narrow-beam attenuation coefficient”
Questions:
1. Exponential attenuation law is suitable only for
a) Photons and neutrons
b) All charged particles
c) Charged and uncharged particle
d) All
Answer:
a) photons and
neutrons
References:
1. http://ozradonc.wikidot.com
5. myweb.dal.ca
6. The physics of Radiation Therapy ,4th
edition by F.M.Khan
Home > Radiation Protection and Quality Assurance > Radiation Physics and Biology > Basic Properties of Radiation
FREE Infographic What successful people believe. What successful people do
Dictionary of Cancer Terms
Need help understanding a word? Here is an electronic resource that gives meaning to Cancer terms and their usage.

StrengthsFinder 2.0
